K-means聚类算法
一、指定需要划分的簇[cù]的个数K值(类的个数)
二、随机地选择K个数据对象作为初始的聚类中心(不一定要是我们的样本点);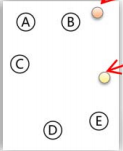
三、计算其余的各个数据对象到这K个初始聚类中心的距离,把数据对象划归到距离它最近的那个中心所处在的簇类中;(数据对象划分到离他近的簇里)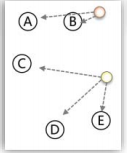
四、调整新类并且重新计算出新类的中心;(计算出新类的中心)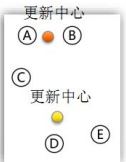
五、循环步骤三和四,看中心是否收敛(不变),如果收敛或达到迭代次数则停止循环;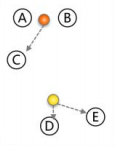
(更新后,C划分到了上面,迭代到收敛)
六、结束。
可以尝试体验的网站:
https://www.naftaliharris.com/blog/visualizing-k-means-clustering/
算法流程推荐使用流程图,避免查重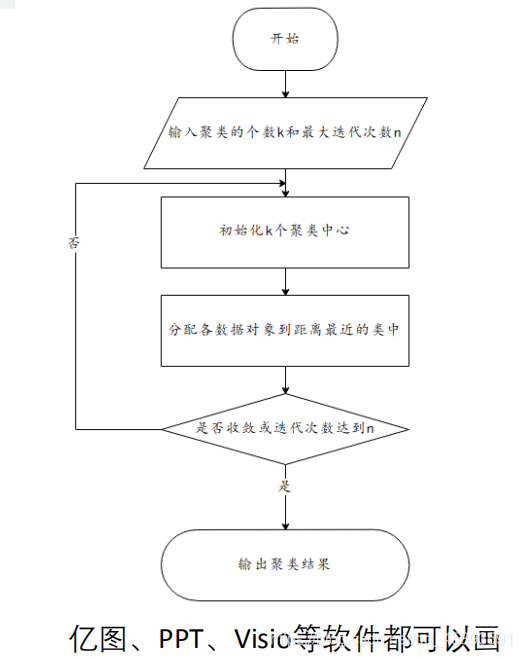
K-means算法优缺点
优点:
(1)算法简单、快速。
(2)对处理大数据集,该算法是相对高效率的。
缺点:
(1)要求用户必须事先给出要生成的簇的数目K。
(2)对初值敏感。
(3)对于孤立点数据敏感。
K‐means++算法可解决2和3这两个缺点
K-means++算法
k-means++算法选择初始聚类中心的基本原则是:初始的聚类中心之间的相互距离要尽可能的远
算法描述如下:
(只对K-means算法“初始化K个聚类中心” 这一步进行了优化)
步骤一:随机选取一个样本作为第一个聚类中心;
步骤二:计算每个样本与当前已有聚类中心的最短距离(即与最近一个聚类中心的距离),这个值越大,表示被选取作为聚类中心的概率较大;最后,用轮盘法(依据概率大小来进行抽选)选出下一个聚类中心;
步骤三:重复步骤二,直到选出K个聚类中心。选出初始点后,就继续使用标准的K-means算法了
spss默认使用K-means++算法
有关K-means++算法问题
(1)聚类的个数K值怎么定?
答:分几类主要取决于个人的经验与感觉,通常的做法是多尝试几个K
值,看分成几类的结果更好解释,更符合分析目的等。
(2)数据的量纲不一致怎么办?
答:如果数据的量纲不一样,那么算距离时就没有意义。例如:如果
X1单位是米,X2单位是吨,用距离公式计算就会出现“米的平方”加
上“吨的平方”再开平方,最后算出的东西没有数学意义,这就有问题了。
(量纲不一致,采用标准差)

系统(层次)聚类
分类准则
样品与样品之间的常用距离(样品i与样品j)

样例
计算指标与指标之间的常用“距离”(指标i与指标j)

样例
类与类之间的常用距离

最短距离法

最长距离法
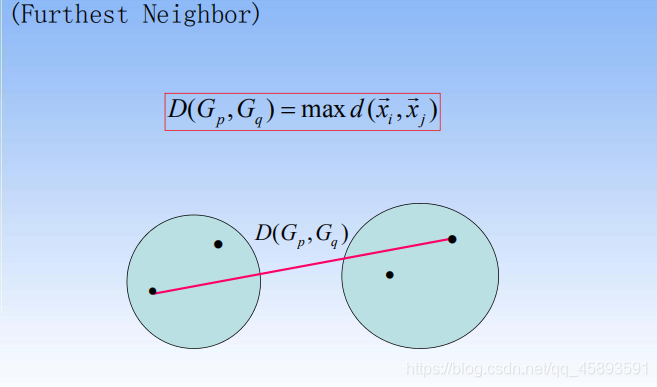
组间平均连接法
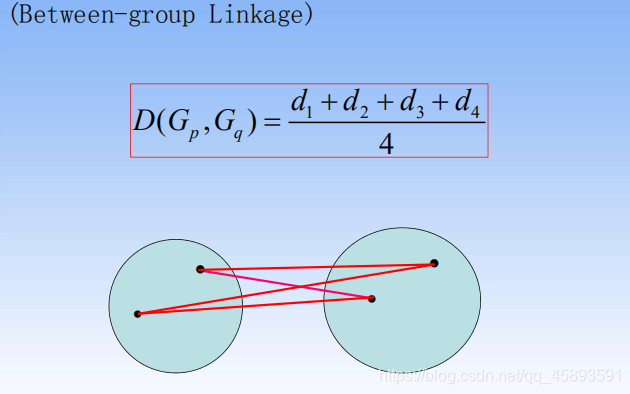
组内平均连接法
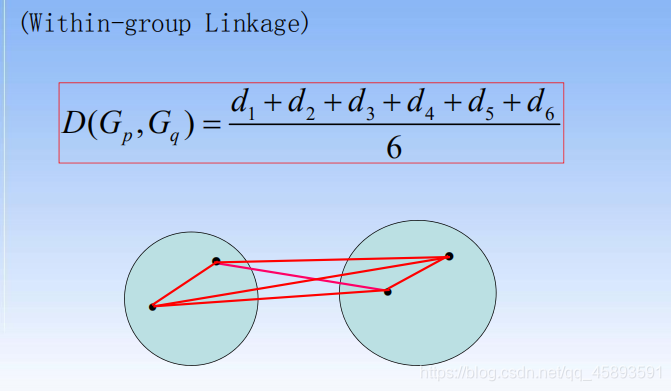
重心法
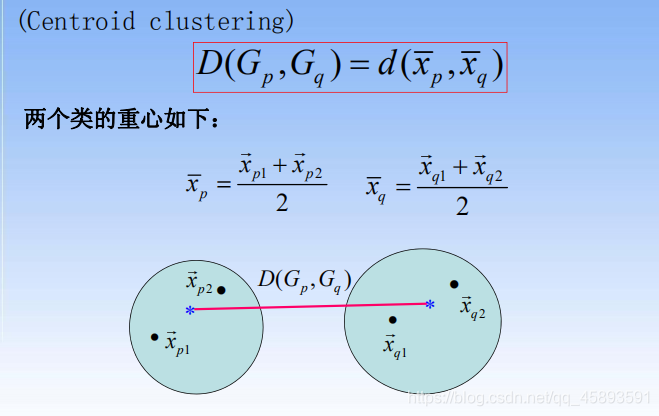
聚类算法流程图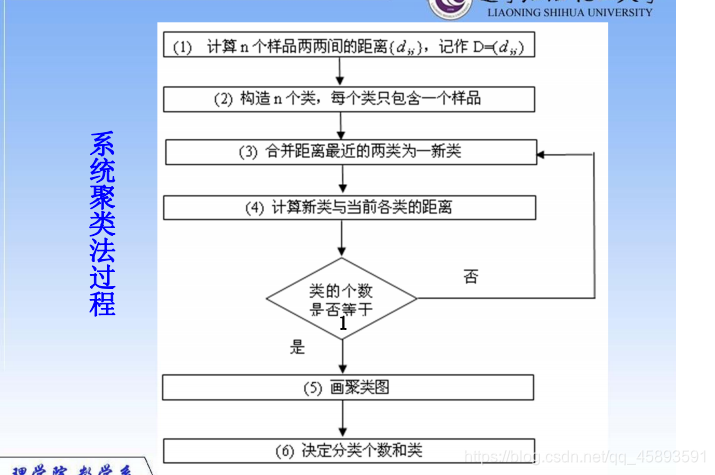
聚类分析需要注意的问题
1.对于一个实际问题要根据分类的目的来选取指标,指标选取的不同分类结果一般也不同。
2.样品间距离定义方式的不同,聚类结果一般也不同。
3.聚类方法的不同,聚类结果一般也不同(尤其是样品特别多的时候)。最好能通过各种方法找出其中的共性。
4.要注意指标的量纲,量纲差别太大会导致聚类结果不合理。
5.聚类分析的结果可能不令人满意,因为我们所做的是一个数学的处理,对于结果我们要找到一个合理的解释。
用图形估计聚类的数量
肘部法则(Elbow Method)(求聚类的数量):通过图形大致的估计出最优的聚类数量
聚合系数折线图的画法
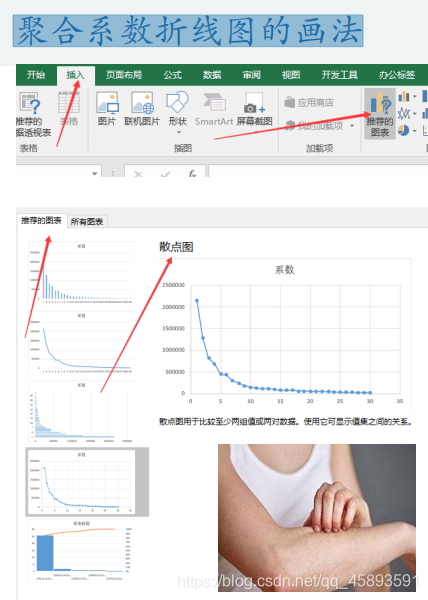
相关的图像分析解释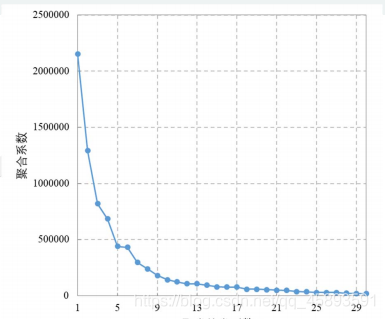
根据图来进行解释:
(1)根据聚合系数折线图可知,当类别数为5时,折线的下降趋势趋缓,故可将类别数设定为5.
(2)从图中可以看出, K值从1到5时,畸变程度变化最大。超过5以后,畸变程度变化显著
降低。因此肘部就是 K=5,故可将类别数设定为5.(当然,K=3也可以解释)
SPSS的具体使用
DBSCAN算法
DBSCAN(Density-based spatial clustering of applications with noise)是Martin Ester, Hans-PeterKriegel等人于1996年提出的一种基于密度的聚类方法,聚类前不需要预先指定聚类的个数,生成的簇的个数不定(和数据有关)。该算法利用基于密度的聚类的概念,即要求聚类空间中的一定区域内所包含对象(点或其他空间对象)的数目不小于某一给定阈值。该方法能在具有噪声的空间数据库中发现任意形状的簇,可将密度足够大的相邻区域连接,能有效处理异常数据。
相关体验链接:https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/
数据分类
• 核心点:在半径Eps内含有不少于MinPts数目的点
• 边界点:在半径Eps内点的数量小于MinPts,但是落在核心点的邻域内
• 噪音点:既不是核心点也不是边界点的点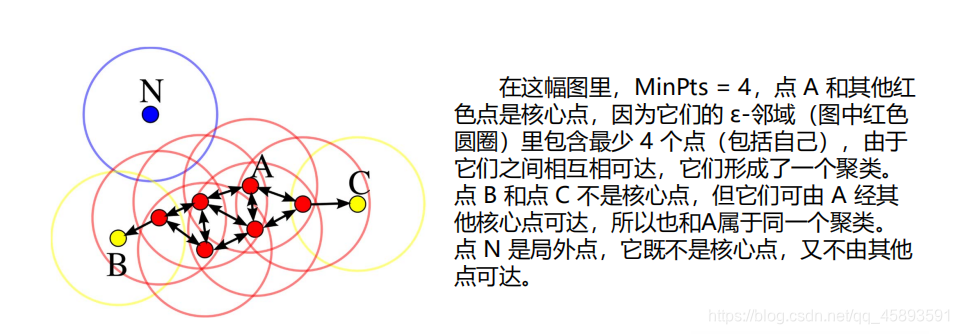
伪代码样例
MATLAB提供的代码教程:
https://ww2.mathworks.cn/matlabcentral/fileexchange/52905‐dbscan‐clustering‐algorithm
DBSCAN算法优缺点
优点:
- 基于密度定义,能处理任意形状和大小的簇;
- 可在聚类的同时发现异常点;
- 与K-means比较起来,不需要输入要划分的聚类个数。
缺点: - 对输入参数ε和Minpts敏感,确定参数困难;
- 由于DBSCAN算法中,变量ε和Minpts是全局唯一的,当聚类的密度不均匀时,聚类距离相差很大时,聚类质量差;
- 当数据量大时,计算密度单元的计算复杂度大。
建议:
只有两个指标,且你做出散点图后发现数据表现得很“DBSCAN”,这时候你再用DBSCAN进行聚类。
其他情况下,全部使用系统聚类吧。
K‐means也可以用,不过用了的话你论文上可写的东西比较少。